General Thermal Design Considerations for a Microwave Applicator

Microwave heating is usually chosen for one or some of the following reasons:

1. the material has low thermal conductivity, so heat does not conduct well into the bulk of the material and thus conventional heating would be slow.
2. microwaves penetrate deep into the material, and deposit significant heat deep in the material where it produces faster and more uniform bulk heating.
3. the walls of the heating vessel can be maintained relatively cool while the interior of the sample is at a temperature well beyond operational range of the vessel material.

The first two conditions generally produce the situation shown in a schematic cross-section in Fig. 1, where, after an initial heating period, the interior of the work-piece is hotter than the outer surface. This is particularly true in batch mode. The outer surface eventually stabilizes at some temperature where the losses to the outer world match the internal heat-flow to the surface. To produce the outwards heat flow, the interior must be hotter than the surface - if it is not, the interior will continue increasing in temperature due to microwave power deposition in the interior!

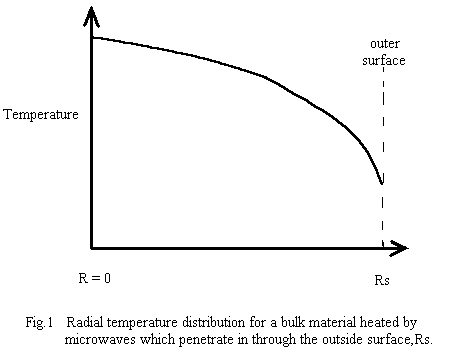
The usual system design requirement is a predictable temperature distribution in the material at the various processing phases . After an initial “run-up” period, the spatial temperature distribution should not change with time. In pure batch-mode microwave heating, the state of thermal equilibrium (ie., constant microwave power deposition and all temperatures stable, including boundaries ) requires that the interior temperature be higher than the exterior (∂T/∂r is negative) so heat can flow outwards to carry away the microwave power deposited in the interior. Also, since the net rate of heat absorption by any small region must be zero, then the magnitude of the temperature gradient must increase with radius ( ie., ∂²T/∂r² is negative (downward curvature) as shown in Fig.1 ).

In continuous processing ( “flow-through”) mode, the above conditions are usually true, especially if the system is moderately well mixed or if the unprocessed material is injected uniformly over the cross-section. However, detailed calculations are necessary, for, in one scenario, control of the rate of injection of cold material can be used to stabilize the temperature distribution rather than using the losses at the boundary.

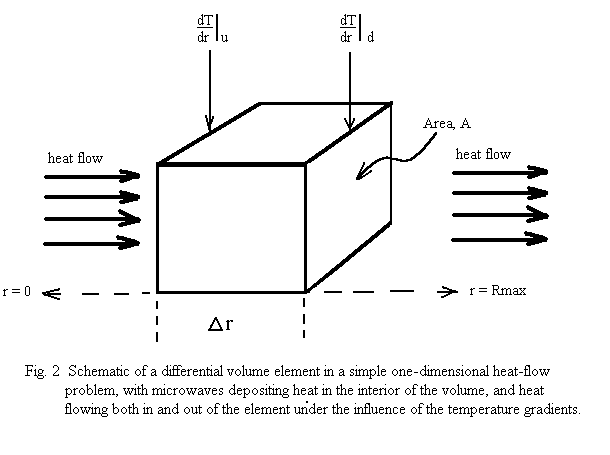
To begin quantifying the general problem, let us first consider very simple approximation - a small rectangular volume in the material (cross-sectional area A, at right angles to the direction of heat flow, and thickness Δr ), and assume simple, one-dimensional, linear heat flow outwards to the boundary (Fig. 2 ). The rate of heat flow through a surface of the volume, ∂Qs(r,t)/ ∂t, is given by

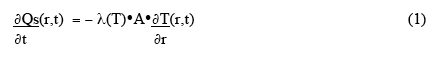
where λ(T) is the thermal conductivity, and outward heat flow is positive. The net rate of heat accumulation in the small volume, ∂Qv(r,t)/∂t , is given by the rate of microwave power deposition in the volume plus the vector sum of the heat-flow through the two surfaces:

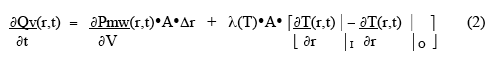
where ∂Pmw(r,t)/ ∂V is the power deposited by the microwaves per unit volume, and the subscripts stand for inner and outer surfaces of the small volume. The net rate of heat gain per unit volume is thus given as:

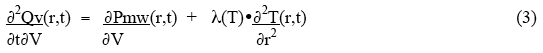
For the condition of thermal equilibrium, ∂²Qv(r,t)/ ∂t∂V = 0 , and the rate of heat loss from a small volume by thermal conduction equals the rate of heat deposition in the small volume by the microwaves. Thus the equilibrium condition becomes:

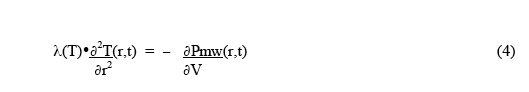
Since the microwave heat deposition is positive, the equilibrium radial temperature distribution must have negative curvature - ie, a downwards curve with increasing radius, as shown in Fig.1. As a simple example, suppose the microwave power deposition is essentially uniform throughout the sample, and has very little temperature dependence. Then the solution for the shape of the equilibrium temperature distribution is :

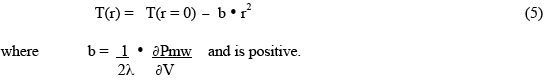
This gives the shape of the distribution (parabolic, downwards), and the temperature difference between the centre (r=0) and the outer wall, but does not tell one the actual value of the central temperature. This must be determined by finding the temperature of the outer wall through the consideration of the boundary conditions which are producing a stable boundary temperature. If the outer surface temperature is not “stabilized” to achieve the desired constant wall temperature, then the interior will continue to get hotter, and “thermal runaway” will occur!

The above equations ( simple, one-dimensional heat flow) were chosen as the simplest way to demonstrate the principles involved. They are easily generalized to 3-dimensional flow, and the principles remain the same, although the specific shape of the radial temperature dependence will change, depending on whether one has cylindrical or spherical (or more complicated) sample geometry.

The system model that one uses to predict if thermal runaway will occur should be the same model used to design the applicator - thermal runaway considerations are just part of the standard applicator design process. Thus the following sections, although written to highlight the influence of specific effects on thermal runaway, are really just the individual design considerations that one eventually integrates into a full system design.

Consideration of Boundary Conditions Which Produce Stable Workpiece Surface Temperatures

When thermal equilibrium is established in a workpiece, the boundary of the system is usually the place where temperature control and stabilization occurs. The internal heat flow and internal microwave energy deposition determine the shape of the interior temperature distribution, but the surface temperature and the rate of loss of heat through the outer sample surface determine when the temperature rise will stop!

To start to quantify the surface behavior, consider a system in which the workpiece (outer surface at position Rs ) is in a container whose walls are at temperature Tw , with a space between the sample surface and the container wall filled with gas ( the gap may, in some cases, be very small if the sample fills the container). The rate of heat loss per unit area by the sample surface to the cooling medium and the container walls beyond the sample is given by

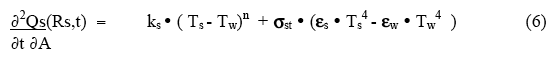
where k_s is the surface convective/conductive loss coefficient, n is a constant (usually equal to one for conductive loss, and sometimes as much as 1.5 for convective loss), and ε_s , ε_w and σ_st are the surface emissivities and the Steffan-Boltzman radiation coefficient. The sample surface can lose heat either by a bulk flow of a gas or liquid over the surface (convection), by random conduction of heat away into the surrounding outside medium ( eg, water or insulating material), or by radiation to the outer wall. At low temperatures ( ‹ 750°C ) the radiation term can usually be neglected relative to the conduction/convection term. However, above 900°C it can rapidly become dominant. For high temperature processing, this can be used as a temperature stabilization mechanism.

The rate of heat flow, per unit area, to the surface from the interior of the sample is given by

where the radial temperature derivative is taken just inside the sample surface. The flow to the surface is equal to the losses by the surface, so

or, written in more explicit terms,

This demonstrates that the time dependent outer surface temperature, T(Rs,t), is directly related to the temperature gradient just inside the sample surface. Under thermal equilibrium conditions, the rate of total heat deposition in the sample (ie., the rate at which microwaves deposit power) is equal to the integral over the surface of the product of the material thermal conductivity near (or at) the surface and the temperature gradient just inside the surface:

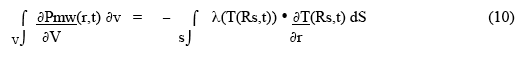
If a chemical reaction is going on in the material, then a rate of reaction heat deposition term ( + if exothermic, - if endothermic) must be included - effectively added to the microwave heat deposition term in the left-hand integral in Eqn. 10 (and also in Eqn. 2, 3, 4 ).

After thermal equilibrium has been established for a batch process, then Eqn. 10 can be used to relate the total power being deposited into the sample to the approximate temperature gradient near the outer wall of the sample. Consider the following example of a sample 3cm diameter and 10cm high ( ~ 100 cm² surface area, ~ 70 cc volume ) with a thermal conductivity of ~30 watt/(m·K) : If half of the power of a home microwave oven (~ 300 watt) is being dissipated in the cylindrical sample, the approximate temperature gradient just inside the surface is ~ 10 degrees Celsius/cm. Thus a very uniform internal temperature distribution with only a few degrees variation over the radius is not possible under equilibrium conditions. The rate of heat loss at the surface is ~ 3 watt/cm². If this is to be dissipated by radiation cooling to room temperature oven walls, the sample surface temperature must be ~ 620 Celsius (assuming surface emissivity ~ 0.85 ). If convective surface cooling provides 1 watt/cm² loss, then the 2 watt/cm² radiation cooling is achieved at ~ 530 Celsius.

Coupling Microwave Power into a Resonant Applicator - the Influence of Dielectric Properties and Cavity Mode Spectrum

A microwave heating system usually has the source of the microwaves located some distance from the applicator, and the microwaves are conducted to the applicator by a waveguide. Even in the home microwave system, the magnetron can be located up to a free-space wavelength ( ~ 12 cm) away from the “oven box”, and a short piece of waveguide connects them. In industrial applications, especially for heating to high temperatures, it is usually necessary to have some distance between the magnetron and the applicator, (1) to be able to insert a protective window to keep material from migrating to the magnetron output coupler, (2) to protect the magnetron body from the high applicator temperatures.

• traveling-wave applicators - in which the applicator is really just a “lossy” extension of the input waveguide ( although often of different transverse dimensions than the waveguide). The microwave power is gradually absorbed by the material as the traveling wave progresses along to the end of the applicator, producing a matched load on the end of the waveguide line which reflects no power. The traveling-wave applicator will not be discussed in this section.
• single mode standing wave applicator - this is a resonant cavity attached to the end of the waveguide line. Over the frequency range of the microwave source ( usually a few megahertz at most), there is only one specific electric/magnetic field spatial distribution that can exist in the cavity. Such a cavity usually has at least two of its dimensions roughly equal to ~ 0.73 of the source-frequency free-space wavelength. For example, at 915 MHz ( free-space λ ~ 33 cm ), a circular cavity in the TM₀₁₀ mode would have a diameter of ~ 25 cm. The practical height ( or length) of such a cavity is often 5 to 15 cm. The result is a cavity of small volume (~ 2 to 5 litres) which is suitable only for processing small samples or volumes of materials.
• multimode standing-wave resonator applicator - this is a large cavity, usually fed by a waveguide line - although in some instances, at very high frequencies, the power source is mounted directly on the cavity. The cavity dimensions are usually a minimum of two to three free-space wavelengths, meaning that many spacial modes can be excited over a small frequency range. This cavity has large volume for large sample batch or continuous processing.

The single mode standing wave applicator

The single mode standing wave applicator is a resonant cavity attached to the end of the waveguide power-feed line. Over the frequency range of the microwave source ( usually a few megahertz at most), there will be one specific electric/magnetic field spatial distribution that can exist in the cavity. At the junction between the waveguide and the applicator, the so-called coupling aperture ( sometimes a coupling loop) regulates the amount of forward power ( ie., power leaving the generator tube and traveling down the line) that enters the cavity. In designing and setting up such a cavity for processing purposes, the topics of cavity frequency dependence and coupling aperture size must be understood.

a) Selection of cavity frequency:

The resonant frequency of the cavity with material in it must be very close to that of the microwave source, and must be maintained there during the material processing. Calculations of the dimensions which will produce the correct resonant frequency must use the correct material dielectric constant values. The problem here is the variation in the dielectric constant as the temperature changes or as the processing progresses. The cavity resonant frequency changes due to material heating and processing, and, unless corrected, the power delivered to the material will change as the cavity resonant frequency shifts relative to the microwave (ie., magnetron) frequency.

Thus, for processing in a single mode cavity, either the frequency of the power source must be changed to keep it at the cavity resonant frequency ( this can be quite a large change if the real part of the dielectric constant of the material varies much with temperature or process time) or some technique must be used to maintain the resonant frequency of the material-filled cavity at exactly the microwave source frequency. Both involve technical challenges for small, high power cavity systems.

b) Coupling aperture considerations:

If the aperture is too small, some of the forward power is reflected and travels back to the magnetron. This condition is called “under-coupled”. This reflected power can cause troubles unless a device called a “circulator” is between the source and the aperture to intercept the reflected power before it re-enters the magnetron. Note that traveling waves going in opposite directions can happily co-exist in a waveguide or on a coax cable. The part of the forward wave that is equal in magnitude to the reflected wave, when summed with the reflected wave, will form a standing wave in the waveguide line. Thus the waves in the waveguide line are a mixture of traveling and standing waves whenever there is some reflected power.

If the coupling aperture is made larger, a size will be reached where no power is reflected - all the forward power enters the cavity and is somehow dissipated! This is called a “critically coupled” system.

If the aperture is opened further, power will again be reflected (back towards the power source) at the coupling aperture, reducing the power transmitted into the cavity. This is called “over-coupled”. The phase of the reflected wave is now 180 degrees different (relative to the forward traveling wave), compared to the under-coupled case.

The ratio of the reflected traveling wave electric field to the forward traveling wave electric field, at or very near the coupling aperture on the wave-guide side of the aperture ( or an integral number of half guide-wavelengths back from it , is called the voltage reflection coefficient, ρ_v . Note that this ratio can be between +1 and -1 , depending on the aperture shape and size. If the end of the wave-guide has a metal plate across it, and the aperture in the plate is very small, then ρ_v ~ -1 (the reflected electric field inverts in direction at a metal surface). If the end of the waveguide is wide open, then ρ_v is positive (although not unity!).

The so-called “coupling coefficient”, β , is given by :

Note: If ρ_v > 0 (ie., positive), the system is over-coupled ( β > 1 ), and there is a voltage maximum in the standing wave in the wave-guide at (or very near to) the coupling aperture (sometimes referred to as the “coupling iris”).

If ρ_v ‹ 0 (ie., negative), the system is under-coupled ( β ‹ 1 ), and there is a voltage minimum in the standing wave in the wave-guide at (or very near to) the coupling aperture.

The question of what specific value of coupling coefficient, β, ( or reflection coefficient, ρ_v ) is produced by a given aperture size and shape depends upon the values of “in phase” (ie., resistive) field impedance (E_t(transverse electric field)/H_t(transverse magnetic “field”) ) on opposite sides of the coupling aperture. The (E_t/H_t) field ratios on the wave-guide side depend largely on the characteristic impedance of the wave-guide at the operating frequency. The “inphase” (E/H) ratios on the cavity side of the aperture depend on the shape and operating mode of the cavity, the size of the aperture, and the square root of the intrinsic Q ( quality factor) of the cavity with the material in it. (The quality factor of the empty cavity is denoted as Q₀ and the contribution of the material denoted by Q_M.)

When building and setting up an actual single-mode microwave applicator, the usual steps involved with adjusting the coupling consist in first measuring the empty cavity Q₀ ( using a very small coupling aperture), and then placing the material in the cavity and measuring the combined Q. (Equation 12 can then be used to determine the value of Q_M , which is useful in later considerations.) The coupling aperture is then cut to the size required for high temperature operation, which can be determined (as will be shown later) using the high temperature value of Q_M (obtained from the high temperature dielectric properties) relative to the value determined at the low temperature where the initial values of Q₀ and Q_M were measured.

If the size of the coupling aperture had been adjusted with the cavity and material at low temperature, then as the value of Q_M drops at higher temperatures, the value of the internal cavity fields decrease (for a given delivered power), and the coupling of the microwaves into the cavity changes. If the aperture was set for critical coupling ( ρ_v = 0 ) at low temperature, then as Q_M decreases, the system becomes under-coupled ( ρ_v ‹ 0 ), and reflected power appears! One way to correct this is to increase the size of the aperture, but then the system will be overcoupled at the low temperature! There are a few techniques to maintain the coupling over a broad operating range, but they are complex and usually expensive at high power. It is usually only necessary to have critical coupling over a narrow operating temperature range as one usually establishes operating temperatures fairly quickly in a system relative to the total processing time.

BASIC MULTIMODE MICROWAVE APPLICATOR DESIGN CONSIDERATIONS

A microwave applicator is the device where microwaves meet and heat the material to be processed. The small group of rf and microwave experts associated with MPN have many years experience in high power applicator design in the frequency range 300 MHz to 3 GHz.

The common household microwave oven (500 to 700 watts average power at 2.45 GHz) is the most widely used (non industrial) microwave applicator. In technical terms it is a rectangular cavity, multimode resonator, used for batch processing. Put simply, it is a metal box whose dimensions are approximately twice the free-space wavelength, so a few different spatial distributions of heating are possible over the operating frequency range. The material is loaded via a door, and is heated for a specific time.

The usual problem with a household oven - and with many industrial applicators - is that the heating pattern is not uniform, and thus the final temperature distribution is not uniform. The reasons for this are as follows, and demonstrate the problems encountered in applicator design.

1. The electric field spatial distribution (ie., the source of the heat ) is inherently sinusoidal(ie., non-uniform) and has peaks at specific locations which change positions as the dielectric constant of the material changes.
2. The strength of the electric field (and thus the heating) is reduced in the interior of a sample because the microwaves are absorbed on the way in.
3. The dielectric constant and the microwave absorption of the material change as the temperature increases, meaning that both of the previously mentioned effects also change with the temperature increase !

For the above reasons, understanding and predicting the temperature distribution in microwave heated material depends upon knowing the temperature dependence of the complex dielectric constant - ie., the real and absorptive parts.

Conventional heating (convective/conductive) is very non-uniform (usually only the surface is heated and the heat must conduct to the interior), and will produce a uniform temperature distribution only if the heating is done very slowly. One of the main advantages of microwave heating is that the heat is deposited in the interior of the sample, avoiding the delay in heat transmission to the interior caused by low thermal conductivity. However, although faster and distributed through the volume, microwave heating is not inherently uniform, and to make use of its high speed in industrial processing usually requires a custom shaped applicator which produces electric field distributions which take into account the material dielectric properties at the processing temperature.

To reduce the electric field non-uniformity problem, it is common practice to move the sample around in the electric field to do some averaging. In batch processing, this is done either by rotating the (solid) material (as in the household oven), or by stirring the (granular or liquid) material during the heating period.

In continuous feed, continuous processing mode, this averaging is usually accomplished by moving the material into the oven , through it , and out at a steady speed , so that each piece sees the same integrated amount of heating - eg., a conveyor belt for solids or a microwave transparent tube for liquids and granular material.

Please feel free to phone or e-mail and discuss possible measurements. We treat all communications as confidential unless advised otherwise.