The following calculation is an example of the steps required in a formal heating calculation. To model a heating problem, the specific values of dielectric constants, external electric field and shape factors are needed.

Heating a Bacon Strip in a 915 MHz Microwave Field

Calculate the temperature achieved in a strip of bacon when heated for 90 seconds in a high power 915 MHz microwave field, assuming no heat loss.

The calculation done here is a very simple, zero order, static calculation of bacon heating in a 915 MHz oven. It assumes no change in values with increasing temperature! It is based on crude estimates, but probably demonstartes the order of magnitude of the parameters and their influence.

1. the dielectric properties of the bacon, as a function of temperature,
2. the average electric field value in the oven and
3. the surface cooling rate.

Assume the bacon has ~ 70% moisture content, and ~ 0.16 M free salts ( low salt bacon).

Assume initial density is ~ 1.5 g/cc, specific heat ~ 0.4cal/(gm*K)

Assume a thin rectangular shape, ~ 20 cm long, 3.0 cm wide , and 3.2 mm thick ( 1/8 inch )

1. Define Specific Values for This Problem

Microwave system frequency definition:

Assumed value of Microwave Electric field value outside the bacon ( this is the approximate value in a household microwave oven):

2. Calculate the Energy Deposit per unit time by the Microwave Field per unit volume in the bacon strip:

Assume that the real part of the dielectric constant is given by approximate numbers taken from the following published measurements:

"Effect of Moisture and Salt Contents on the Dilelctric Behaviour of Liquid and Semi-solid Foods"

S. Swami et al., Dept. of Food engineering, Univ. of Mass., Amherst 1981 Microwave Power Symposium Digest, Pg. 248 - 250

Calculate what the approximate microwave electric field is inside the bacon strip:

The field inside the bacon depends on the angle of incidence of the "travelling wave" and on the polarization of the "wave" - ie., on whether the electric field is parallel to the surface ( Fsh < 0.1 ) or perpendicular to the surface ( Fsh ~ 1 ). In the approximate standing wave situation inside an oven there is a supperposition of the two forms, so we assume an electric field composed of two perpendicular components, each "square root of two" smaller than the average value

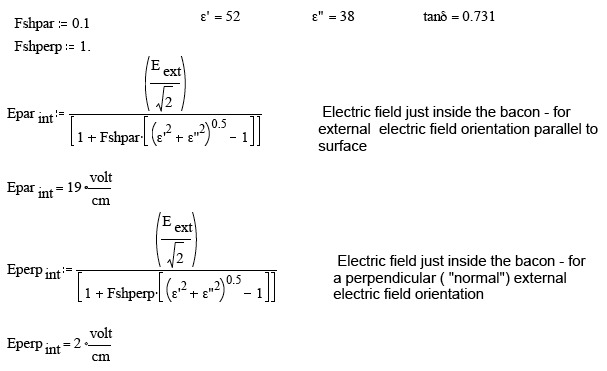
The following formula is used to calculate the microwave power delivered as heat per unit volume of material

If the bacon is in the electric field for a time increment Δt of 90 seconds, then what is the temperature rise, assuming no heat loss from the surface?

Energy deposit in bacon strip during time Δt is :

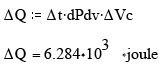
Temperature rise in time Δt, assuming no loss , is ΔT

To summarize, for a heating time of Δt = 90 sec with oven electric field =

the temperature rise in time Δt, is    ΔT = 130•K Celcius degrees for a heating rate of

Celcius degrees per second.

Please feel free to phone or e-mail and discuss possible measurements. We treat all communications as confidential unless advised otherwise.