1. General Introduction to Thermal Runaway:

The first step in understanding and quantifying “thermal runaway” is to have a clear definition of what it means in relation to microwave heating systems.

The general intuitive definition is that thermal runaway is a rapid, continuous and uncontrolled rise in temperature, generally in the interior of the sample, with the eventual destruction of the sample as a useful product. Although this has a graphic gut appeal, it isn`t a very useful definition when designing a system! Often the system in which such an event has occurred was not designed and numerically modeled, and no inherent stability mechanism was invoked to regulate the temperature distribution in the material. Here, the word “in” is important. We are intuitively conditioned to understand heating as conventional heating, where, in general, the outer surface is always hotter than the interior when actively heating the material, and where a simple measurement of surface temperature tells us the maximum temperature in the material. This is where we go wrong when first introduced to microwave heating!

In microwave heating, the microwaves deposit heat continuously throughout the depth of the material, in varying amounts, depending on the spatial distribution of the complex dielectric constant – which depends somewhat on the temperature distribution. Since the heat loss is only at the outer surface, eventually the outer surface becomes the coolest part of the material! Once this is understood, the simple operational assumption is often made that the thermal conductivity will be high enough to keep the interior temperature reasonably close to the surface temperature - which may not be the case for (1) low thermal conductivity materials or (2) for materials where the heat absorption per unit volume increases rapidly with temperature .

Another problem with the intuitive definition is that the temperature rise which constitutes “thermal runaway” and results in destruction of a region of the sample, can take several hours to occur. The time-scale of the event depends on the size of the work-piece, the specific heat, the local value of the thermal conductivity and the maximum possible microwave power delivered to a region.

Consider the following situation:

Case 1 : A block of material is placed in a microwave oven for an hour during which the surface temperature rises to 800ºC and then stays constant. After cooling the sample, it is found that the interior got up to 1200ºC and ruined the internal material properties. This is a processing disaster, but should only be considered thermal runaway if the predicted (calculated) interior temperature was much lower than 1200ºC. If such is the case, the likely problem was the assumed value of the thermal conductivity ( too low!) or the temperature dependence of the complex dielectric constant used in the calculation! Too much heat remained in the interior!

Case 2 : As a second example, consider a large ( ~ 2 metre diameter ) fluidized powder bed, which should have large effective thermal conductivity ( fluidized beds are known to have this property), and whose outer surface is monitored and is to be maintained at 700ºC. After startup and a few hours running, everything looks fine and the temperature on the outer wall is stabilizing at 700ºC. Then the reverse power starts a slow gradual increase (assuming it was minimized after start-up). The system is shut down for inspection, and a small melted/reformed region is found in the interior, at some distance from the walls. In this case, the thermal conductivity of the material in the local region was much smaller than expected, and the region increased slowly to a high temperature, with associated increase in local microwave absorption and eventual melting. However, relative to the absorption in the whole bed, the increase in total absorbed power was small, and thus had only a modest and slow influence on the reverse (reflected) power. Temperature control via the reverse power signal was too late! This situation is closer to what one would intuitively call “thermal runaway”, and the problem is that the design calculations did not include the “stagnant” or “low gas flow” region that existed around a feed pipe in the large applicator, and caused low local thermal conductivity values.

The following is a practical definition of thermal runaway, which leads one towards identifying the sources of thermal runaway in real processes:

“Thermal Runaway” is the situation when the temperature in a region of the microwave-heated material increases significantly above the calculated operating temperature, which was determined in the design of the process system.”

This definition assumes that the system has been (numerically) designed to achieve a specific spatial temperature distribution with a specific time-dependence under stable, controllable operating conditions. Experience has shown that the “system” referred to here must include the microwave power feed-line and source, which are usually “intimately” (ie., strongly) coupled to the applicator and thus to the sample inside the applicator. If thermal runaway occurs, then, given that the design calculations did not have numerical errors, the conclusion must then be that the design calculations did not include some critical mechanism or that some of the numerical values used in the calculations were not the actual, real material or system values.

Note that this definition states that the object of the design was a controllable, stable temperature distribution - either (a) time dependent, as in batch processing cases where the temperature is usually required to ramp up in a controlled fashion to a stable process temperature, or (b) time independent, as in continuous feed of a material through a process applicator. This means that a system has to be deliberately designed to achieve the required stability using one or more techniques.

The following are examples of various methods of temperature control and stabilization.

• Sense the temperature of the material (one or many sensors), and control the output of the microwave power source to achieve the required temperature-versus-time curve. (Continuous or Batch)
• Keep the microwave power delivered to the material constant by measuring and regulating the difference between the forward and reverse power. ( Continuous or Batch )
• Sense the temperature of the material (one or many sensors), keep the forward power constant, and control the material flow rate to achieve the required temperature. (Continuous)

These and other techniques place specific requirements on one or more of the system components to achieve stability.

In example (a), if a rapid rise to process temperature is required, then the time constant of the sensors must be short enough and the response time of the power supply must be fast enough for stable control. If surface temperature sensors are used, then the relationship between surface and interior temperature, which is both time and temperature dependent, must be known, to control interior temperatures ( which are often not measurable).

In example (b), stable operation will only be attained if the heat loss mechanisms ( conduction, radiation) do not change with time. This also requires that the thermal conductivity of the material must not change, especially in a long hold in a batch process. In many cases where radiation heat loss from surfaces is significant, the rapid increase of radiation losses with temperature can be used as a mechanism for stabilizing the surface temperature ( because an increase in surface temperature would require a large increase in delivered power).

In example (c), the density of the material may change with time (clumping or aggregation), or have local variations in it (voids or vortices or stagnant regions ), leading to variations in local values of thermal conductivity and specific heat. The magnitude of these effects is important to the determination of the stability of the temperature distribution.

1. The rate at which the microwaves deposit energy into the material, as a function of position, time and temperature in the material. The first necessary ingredient to this calculation is the temperature dependence of the complex dielectric constant of the material at all stages of processing, both so that the local power deposition rate can be determined, and also so that the distribution of microwave electric field overall in the material can be determined! The later is often crudely determined by using the half-power depth for microwave absorption, which can be calculated from the complex dielectric constant values. Another input to the calculation is the effect of the changing dielectric properties on the amount of forward power on the feed-line that is actually dissipated in the sample - ie., on the coupling constant between the feed-line and the cavity.
2. The rate at which heat is transferred through the material by the temperature gradients. This requires knowing the thermal conductivity as a function of temperature and (for powders and mixes) of material density.
3. The temperature produced by a specified total heat input to the material. Usually the specific heat is not a strong function of temperature, and a reasonable estimate based on material type is sufficient. However, any phase transitions in the material can have a strong influence in the temperature range near the phase transition.

As outlined above, a study of whether thermal runaway can happen in a system must be based on a detailed consideration of the individual factors that go into the microwave heating system design, and then on the overall integrated performance of the system. The following sections will first discuss general microwave-heating system design, and then discuss what boundary conditions help to produce a stable temperature distribution.

2. General Thermal Design Considerations for a Microwave Applicator:

1. the material has low thermal conductivity, so heat does not conduct well into the bulk of the material and thus conventional heating would be slow.
2. microwaves penetrate deep into the material, and deposit significant heat deep in the material where it produces faster and more uniform bulk heating.
3. the walls of the heating vessel can be maintained relatively cool while the interior of the sample is at a temperature well beyond operational range of the vessel material.

The first two conditions generally produce the situation shown in a schematic cross-section in Fig. 1, where, after an initial short transient heating period ( which depends on the thermal conductivity of the material and on the microwave penetration depth), the interior of the workpiece is hotter than the outer surface. This is particularly true in batch mode. The outer surface eventually stabilizes at some temperature where the losses to the outer world match the internal heat-flow to the surface. To produce the outwards heat flow, the interior must be hotter than the surface - if it is not, the interior will continue increasing in temperature due to microwave power deposition in the interior!

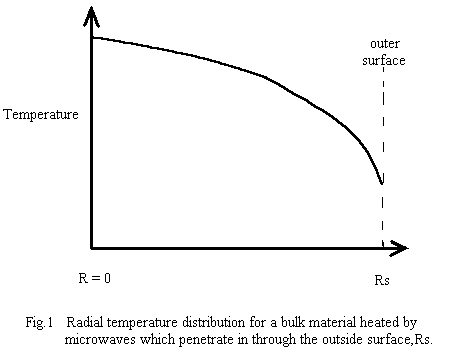
The usual system design requirement is a predictable temperature distribution in the material at the various processing phases . After an initial “run-up” period, the spatial temperature distribution should not change with time. In pure batch-mode microwave heating, the state of thermal equilibrium (ie., constant microwave power deposition and all temperatures stable, including boundaries ) requires that the interior temperature be higher than the exterior (∂T/∂r is negative) so heat can flow outwards to carry away the microwave power deposited in the interior. Also, since the net rate of heat absorption by any small region must be zero, then the magnitude of the temperature gradient must increase with radius ( ie., ∂²T/∂r² is negative (downward curvature) as shown in Fig.1 ).

In continuous processing ( “flow-through”) mode, the above conditions are usually true, especially if the system is moderately well mixed or if the unprocessed material is injected uniformly over the cross-section. However, detailed calculations are necessary, for, in one scenario, control of the rate of injection of cold material can be used to stabilize the temperature distribution rather than using the losses at the boundary.

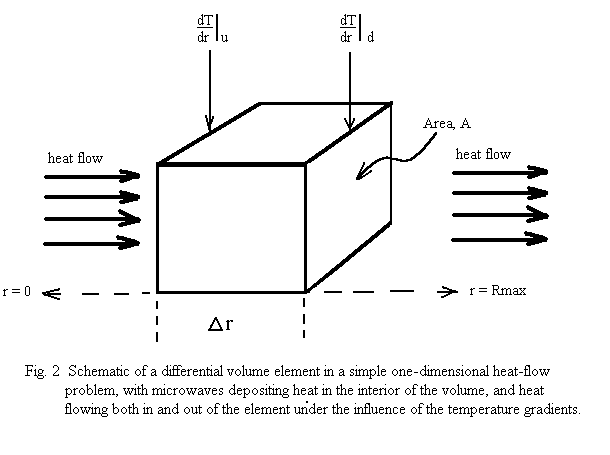
To begin quantifying the general problem, let us first consider very simple approximation - a small rectangular volume in the material (cross-sectional area A, at right angles to the direction of heat flow, and thickness Δr ), and assume simple, one-dimensional, linear heat flow outwards to the boundary (Fig. 2 ). The rate of heat flow through a surface of the volume, ∂Qs(r,t)/ ∂t, is given by

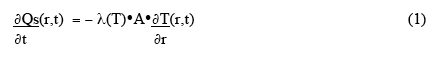
where λ(T) is the thermal conductivity, and outward heat flow is positive. The net rate of heat accumulation in the small volume, ∂Qv(r,t)/∂t , is given by the rate of microwave power deposition in the volume plus the vector sum of the heat-flow through the two surfaces:

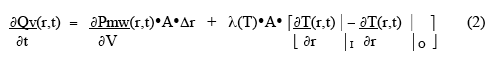
where ∂Pmw(r,t)/ ∂V is the power deposited by the microwaves per unit volume, and the subscripts stand for inner and outer surfaces of the small volume. The net rate of heat gain per unit volume is thus given as:

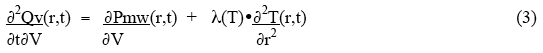
For the condition of thermal equilibrium, ∂²Qv(r,t)/ ∂t∂V = 0 , and the rate of heat loss from a small volume by thermal conduction equals the rate of heat deposition in the small volume by the microwaves. Thus the equilibrium condition becomes:

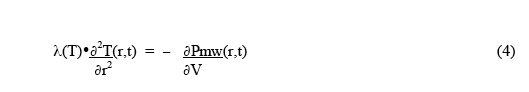
Since the microwave heat deposition is positive, the equilibrium radial temperature distribution must have negative curvature - ie, a downwards curve with increasing radius, as shown in Fig.1. As a simple example, suppose the microwave power deposition is essentially uniform throughout the sample, and has very little temperature dependence. Then the solution for the shape of the equilibrium temperature distribution is :

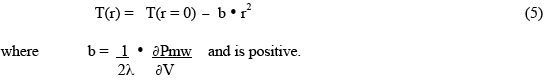
This gives the shape of the distribution (parabolic, downwards), and the temperature difference between the centre (r=0) and the outer wall, but does not tell one the actual value of the central temperature. This must be determined by finding the temperature of the outer wall through the consideration of the boundary conditions which are producing a stable boundary temperature. If the outer surface temperature is not “stabilized” to achieve the desired constant wall temperature, then the interior will continue to get hotter, and “thermal runaway” will occur!

The above equations ( simple, one-dimensional heat flow) were chosen as the simplest way to demonstrate the principles involved. They are easily generalized to 3-dimensional flow, and the principles remain the same, although the specific shape of the radial temperature dependence will change, depending on whether one has cylindrical or spherical (or more complicated) sample geometry.

The system model that one uses to predict if thermal runaway will occur should be the same model used to design the applicator - thermal runaway considerations are just part of the standard applicator design process. Thus the following sections, although written to highlight the influence of specific effects on thermal runaway, are really just the individual design considerations that one eventually integrates into a full system design.

Consideration of Boundary Conditions Which Produce Stable Workpiece Surface Temperatures

When thermal equilibrium is established in a workpiece, the boundary of the system is usually the place where temperature control and stabilization occurs. The internal heat flow and internal microwave energy deposition determine the shape of the interior temperature distribution, but the surface temperature and the rate of loss of heat through the outer sample surface determine when the temperature rise will stop!

To start to quantify the surface behavior, consider a system in which the workpiece (outer surface at position Rs ) is in a container whose walls are at temperature Tw , with a space between the sample surface and the container wall filled with gas ( the gap may, in some cases, be very small if the sample fills the container). The rate of heat loss per unit area by the sample surface to the cooling medium and the container walls beyond the sample is given by

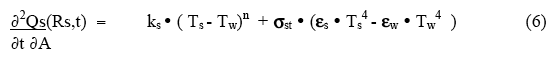
where k_s is the surface convective/conductive loss coefficient, n is a constant (usually equal to one for conductive loss, and sometimes as much as 1.5 for convective loss), and ε_s , ε_w and σ_st are the surface emissivities and the Steffan-Boltzman radiation coefficient. The sample surface can lose heat either by a bulk flow of a gas or liquid over the surface (convection), by random conduction of heat away into the surrounding outside medium ( eg, water or insulating material), or by radiation to the outer wall. At low temperatures ( ‹ 750°C ) the radiation term can usually be neglected relative to the conduction/convection term. However, above 900°C it can rapidly become dominant. For high temperature processing, this can be used as a temperature stabilization mechanism.

The rate of heat flow, per unit area, to the surface from the interior of the sample is given by

where the radial temperature derivative is taken just inside the sample surface. The flow to the surface is equal to the losses by the surface, so

or, written in more explicit terms,

This demonstrates that the time dependent outer surface temperature, T(Rs,t), is directly related to the temperature gradient just inside the sample surface. Under thermal equilibrium conditions, the rate of total heat deposition in the sample (ie., the rate at which microwaves deposit power) is equal to the integral over the surface of the product of the material thermal conductivity near (or at) the surface and the temperature gradient just inside the surface:

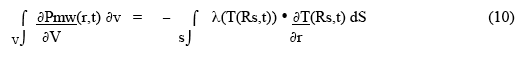
If a chemical reaction is going on in the material, then a rate of reaction heat deposition term ( + if exothermic, - if endothermic) must be included - effectively added to the microwave heat deposition term in the left-hand integral in Eqn. 10 (and also in Eqn. 2, 3, 4 ).

After thermal equilibrium has been established for a batch process, then Eqn. 10 can be used to relate the total power being deposited into the sample to the approximate temperature gradient near the outer wall of the sample. Consider the following example of a sample 3cm diameter and 10cm high ( ~ 100 cm² surface area, ~ 70 cc volume ) with a thermal conductivity of ~30 watt/(m·K) : If half of the power of a home microwave oven (~ 300 watt) is being dissipated in the cylindrical sample, the approximate temperature gradient just inside the surface is ~ 10 degrees Celsius/cm. Thus a very uniform internal temperature distribution with only a few degrees variation over the radius is not possible under equilibrium conditions. The rate of heat loss at the surface is ~ 3 watt/cm². If this is to be dissipated by radiation cooling to room temperature oven walls, the sample surface temperature must be ~ 620 Celsius (assuming surface emissivity ~ 0.85 ). If convective surface cooling provides 1 watt/cm² loss, then the 2 watt/cm² radiation cooling is achieved at ~ 530 Celsius.

Please feel free to phone or e-mail and discuss possible measurements. We treat all communications as confidential unless advised otherwise.