Beryllia (> 99.5% purity), Sintered, ρ = 2.86 g/cc
Solid Beryllia (>99.5% purity):
Measurements from 25ºC to 1425ºC, over a low frequency range (54 MHz to 600 MHz, and a high frequency range (397 MHz to 2986 MHz)
These measurements were made as a collaborative project. MPN performed the dielectric properties measurements and data analysis. G. Del Regno of AMPS, LLC provided the test samples; and Dr. H. Gieshe of Alfred University provided the CTE measurements of this material from 25 ºC to 1800ºC. The CTE data was required to improve the accuracy of the dielectric properties data analysis at high temperatures, where accurate sample dimensions are required.
The Beryllia (BeO) samples were made from extruded rod, fired at 1550ºC, and then were precision machined to high tolerances. The material density was measured to be 2.86 g/cc, or 95.0% of theoretical density (3.01 g/cc). Typically, extruded rod will have lower density when compared with other forming methods, so 95.0% of theoretical density is typical for this size extrusion. The material was produced in the late 1990s by General Ceramics, a once publicly traded company which no longer exists, but which was reincarnated as American Beryllia Incorporated.
The powder from which this extruded material was made came from Brush-Wellman Company, who has since changed their name to Materion Incorporated. They are located in Phoenix, Arizona. The powder is sold as their UOX grade and specified at 99.5% purity. However, ICP, XRD, and XRF analysis performed on the raw powder suggests its purity is actually closer to 99.9%.
The measurements were done using GE 214 high purity amorphous silica holders, with a thin base which had an ~ 1 mm diameter hole in it, so pure, artifical, air could be flowed up past the sample ( flow rate ~ 10 sccm – standard cubic centimeters per minute) during the measurement, reducing the possibility of atmosphere effects.
Standard calibrations were done, using copper, sapphire, and Teflon samples at the beginning of each run.
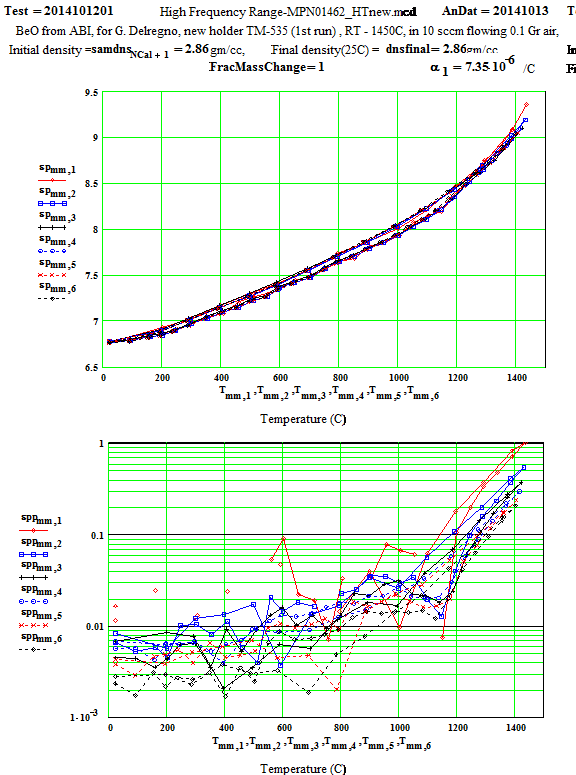
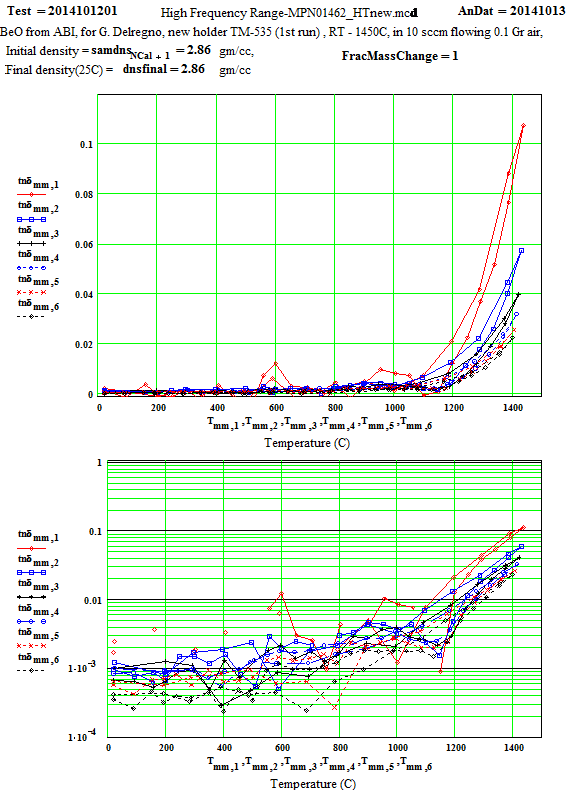
High Frequency Range ( 397 MHz to 2986 MHz)
The test sample was simply placed in the 4 mm ID holder, and the run done in 50ºC steps up to 1450ºC, then 1400ºC. Then the temperature was stepped back down in -100ºC steps to 200 ºC, then room temperature, with measurements made during the cool-down. After each step, the temperature was held for ~ 6 minutes to allow the temperature in the sample to stabilize and become uniform.
After the run the sample was removed, and the empty holder measured again up to high temperature to determine the empty sample holder subtractions, and to test for contamination.
The initial high-frequency sample parameters were:
- diameter 3.49 +/- 0.05 mm
- length 12.00 +/- 0.05 mm
- mass 0.328 +/- 0.002 gm
- room temperature density 2.86 +/- 0.10 gm/cc.
- appearance - white ceramic rod
The final sample properties, at room temperature were identical to the initial values.
For the data analysis, the measured thermal expansion coefficient was fitted in three segments over the measurement temperature range:
a= 7.35 *10-6/K, 25 ºC to 800ºC
a= 11.28 *10-6/K, 800 ºC to 1100ºC
a= 12.71 *10-6/K, 1100 ºC to 1450ºC
These values were used to determine the sample dimensions at each measurement temperature in the following way.

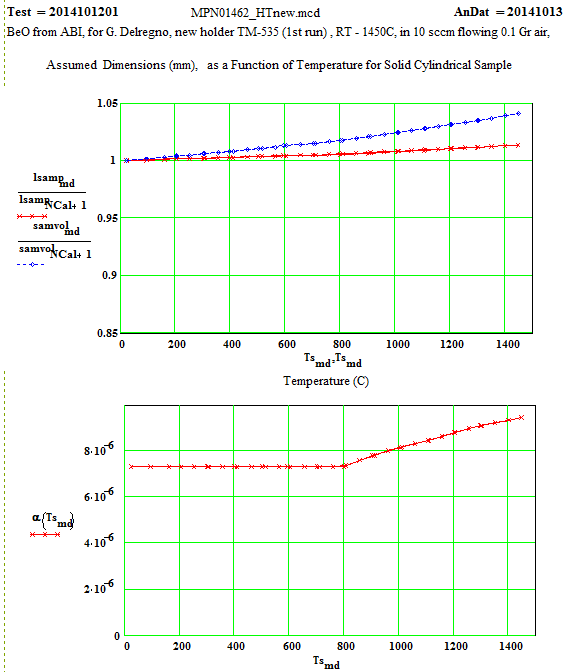
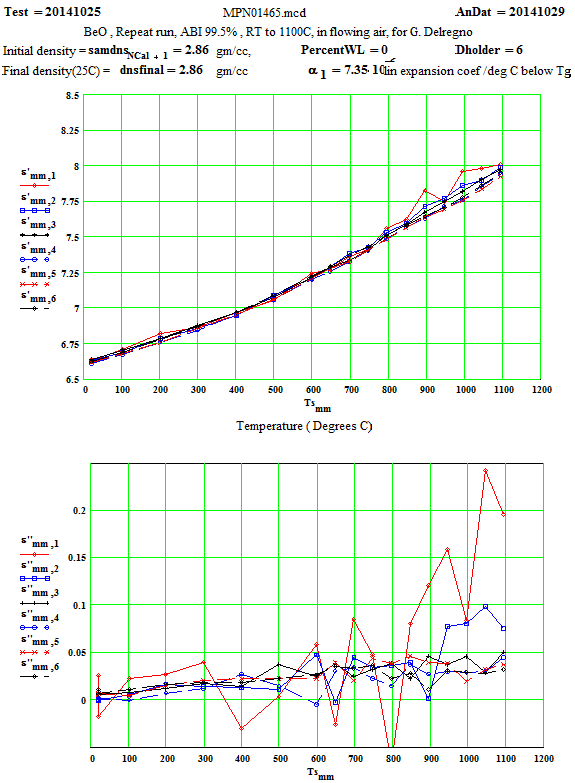
(Above) Plot of sample length and volume relative to initial values at room temperature.
(Below) Plot of values of effective CTE as a function of sample temperature, based on values measured by Dr. H. Gieshe, Alfred Univsersity.
Discussion of Results:
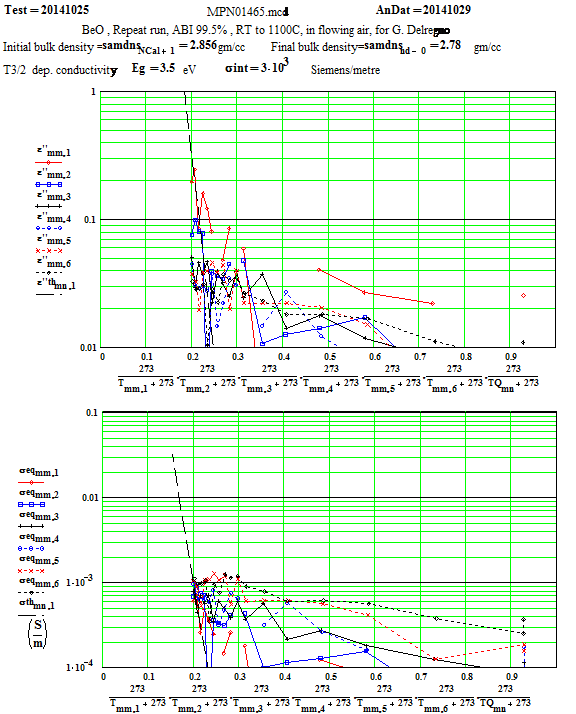
The slight difference in ε′ values between the ramp up in temperature and the ramp down of temperature is likely a good indicator of the overall error in our measurements, as the effects include the difference between empty holder subtractions during the ramp up compared to the ramp down (see our measurements on fused quartz under our ‘Glass’ section), and slight differences in temperature between the sample (in the interior of the holder) and the thermocouples (just outside the holder).
The difference in ε′ values between the room temperature high frequency and low frequency range (~ 3%) is probably a good indicator of the absolute errors in our calibrations and our data analysis equations, considering that two radically different cavities and sample sizes were used for the two measurements!
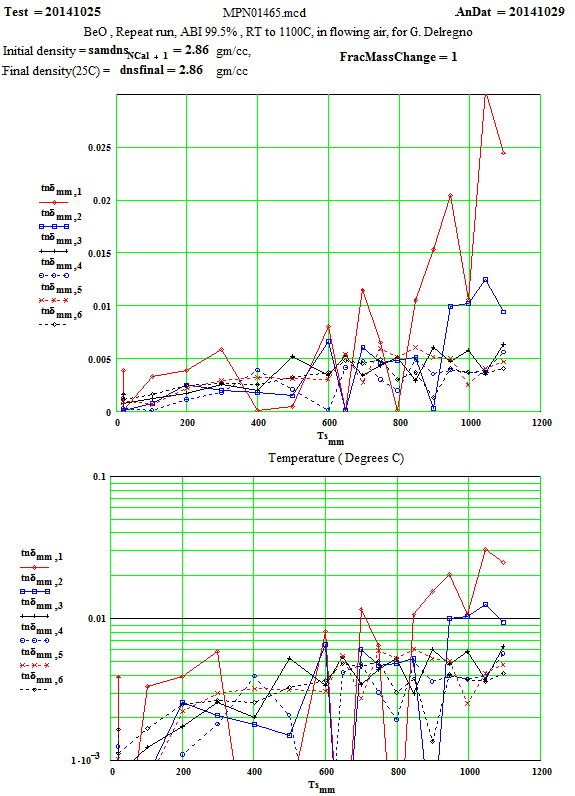
The values of ε′′ for the 397 MHz (and to a lesser extent for the 912 MHz peak) have some scatter caused by noise on the low signal levels (which is largest for the lowest frequency). The random error equates to an error in ε′′ of approximately ±0.02 for the
397 MHz values and ±0.01 for the 912 MHz values. Thus, especially at low temperatures, averaging (i.e., running a line through the data for each frequency as a function of temperature) can produce realistic reasonable low temperature values for ε′′ for these frequencies, although with large error bars!
The Arrhenius plot of determined equivalent conductivity suggests that, above 1280ºC, the loss mechanism is free electron conduction, as the equivalent conductivity is frequency independent (conduction electron conductivity is frequency independent).
Legend for High Frequency Data Plots:
# Frequency (MHz) Symbol
1 397 red diamond, solid line
2 912 blue square, solid line
3 1429 black cross, solid line
4 1948 blue circle, dotted line
5 2466 red cross, dotted line
6 2986 black diamond, dotted line

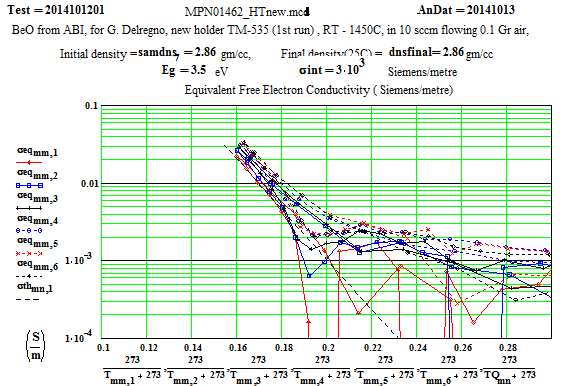
Low Frequency Range ( 54 MHz to 600 MHz)
The low frequency test sample was placed in the 6mm ID holder, and the test performed in 50ºC increments up to 1100ºC (The furnace used on the low frequency system has a maximum operating use temperature of 1150ºC). The temperature was subsequently stepped back down in -100ºC increments to 200 ºC, then room temperature, with measurements made during the cool-down. After each step, the temperature was held for ~ 6 minutes to allow the temperature in the sample to stabilize and become uniform.
After each test the sample was removed, and the empty holder was again measured at high temperature to determine the empty sample holder subtractions, and to test for contamination.
The initial high-frequency sample parameters were:
- diameter 5.49+/- 0.05 mm
- length 30.00 +/- 0.05 mm
- mass 2.028 +/- 0.002 gm
- room temperature density 2.86 +/- 0.10 gm/cc.
- appearance - white ceramic rod
The final sample properties, at room temperature were identical to the initial values.
Discussion of Low Frequency Results:
The values of ε′′ for the 54 MHz (and to a lesser extent for the 163 MHz peak) have some scatter caused by noise on the low signal levels (which is largest for the lowest frequency). The random error equates to an error in ε′′ of approximately ±0.02 for the 54 MHz values and ±0.01 for the 163 MHz values. Thus, especially at low temperatures, averaging (i.e., running a line through the data for each frequency as a function of temperature) can produce realistic reasonable low temperature values for ε′′ for these frequencies, although with large error bars!
The theoretical Arrhenius-based values of equivalent conductivity, calculated using the parameters fitted for the high frequency run, are shown here on the low frequency plots of equivalent conductivity. The scatter in the measured values is large, but the values are consistent with the theoretical fits to the high frequency values.
Legend for Low Frequency Data Plots:
# Frequency (MHz) Symbol
1 54 red diamond, solid line
2 163 blue square, solid line
3 272 black cross, solid line
4 381 blue circle, dotted line
5 490 red cross, dotted line
6 599 black diamond, dotted line
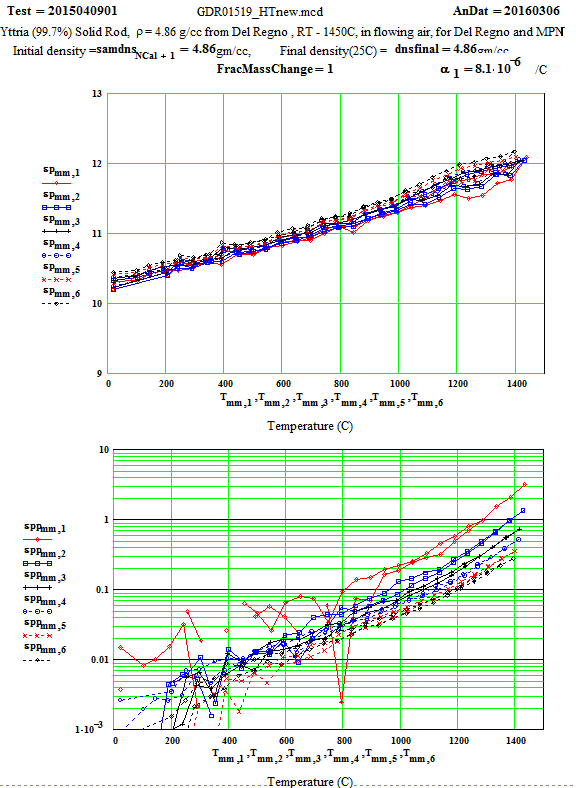
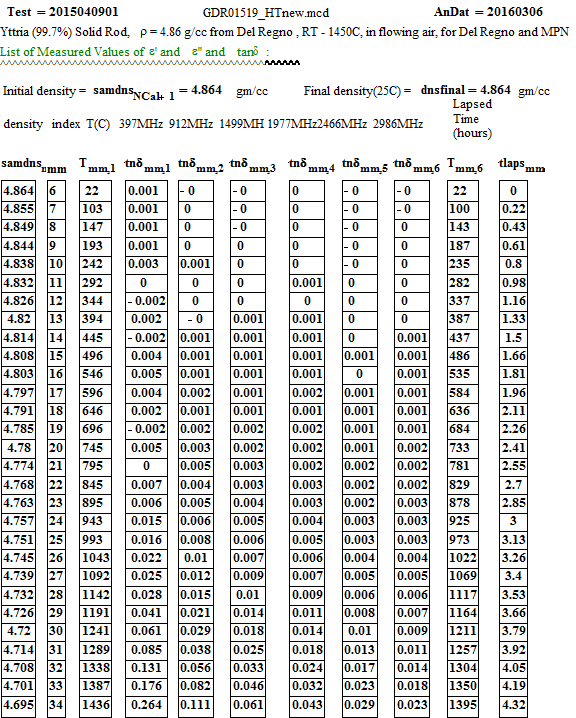
Yttria ( 99.7% ) Solid Sample
Solid Yttria (99.7% purity) supplied by Mitsui, Japan: from 25ºC to 1400ºC
This measurement was a collaborative project by MPN and G. Del Regno of AMPS,LLC, who obtained the test sample.
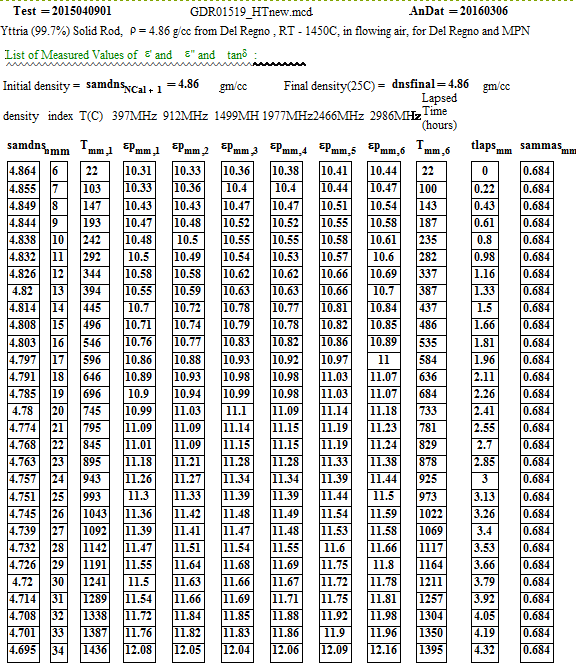
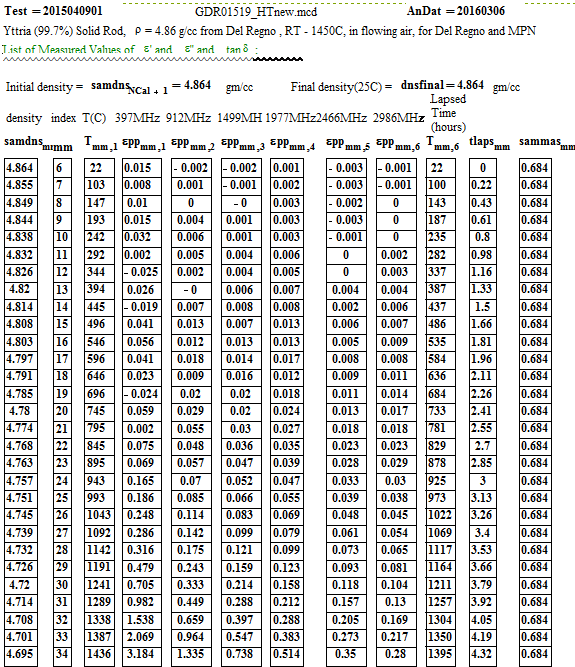
The measurement sample was made by diamond core-drilling the small solid fired disc made by Mitsui. The results of core-drilling were not perfect, for the material seemed brittle, and cracked easily – making it impossible to get a full length ( 12 mm) cylindrical sample. Two cylinders, one ~ 10.5 mm long and the other ~ 4.5 mm long were stacked to form the measurement sample. We carefully measured the sample dimensions, weighed the sample, and determined the density was 4.86 ± 0.20 g/cc, fairly close to the crystalline value of 5.01 g/cc.
The measurement was done using a GE 214 high purity amorphous silica holder, with a base with an ~ 1 mm diameter hole in it, so air could be flowed up past the sample ( flow rate ~ 10 sccm – standard cubic centimeters per minute) during the measurement, reducing the possibility of reducing atmosphere effects.
Standard calibrations were done, using copper, sapphire and Teflon samples at the beginning of the run.
Following this, the two pieces of test sample were simply placed in the holder, and the run done in 50ºC steps up to 1450ºC, then 1400ºC. Then the temperature was stepped back down in -50ºC steps, and measurements made during the cool-down. After each step, the temperature was held for ~ 6 minutes to allow the temperature in the sample to stabilize and become uniform.
After the run the sample was removed, and the empty holder measured again up to high temperature to determine the sample holder subtractions.
The initial ‘effective’ sample parameters were:
a) diameter 3.52 ± 0.05 mm
b) length 14.45 +- 0.5 mm
c) mass 0.684 +- 0.002 gm
d) room temperature density 4.86 ± 0.20 gm/cc.
e) appearance - two cream-coloured ceramic rods
The final sample properties, at room temperature were identical to the initial values.
For the data analysis, a value of the thermal expansion coefficient, a= 8.1 *10-6/K, was used up to 1000ºC. Above 1000ºC, the value was increased to 9.0*10-6/K . This is a compromise average number, as the value is slightly dependent on temperature.
Discussion of Results:
The low temperature values of ε′′ ( up to 800ºC) for the 397 MHz and 912 MHz peaks have some scatter because there is random noise on the signals (which is largest for the lowest frequency). The random error equates to an error in ε′′ of approximately ±0.02 for the 397 MHz values and ±0.01 for the 912 MHz values. Thus averaging ( ie., running a line through the data for each frequency as a function of temperature) can produce realistic reasonable low temperature values for ε′′ for these frequencies, although with large error bars!
The Arrhenius plot of determined equivalent conductivity suggests that, above 1280ºC, the loss mechanism is free electron conduction, as the equivalent conductivity is frequency independent ( conduction electron conductivity is frequency independent).
The frequency coding is :
Legend for Data Plots :
# Frequency(MHz) Symbol
1 397 red diamond, solid line
2 912 blue square, solid line
3 1429 black cross, solid line
4 1948 blue circle, dotted line
5 2466 red cross, dotted line
6 2986 black diamond, dotted line
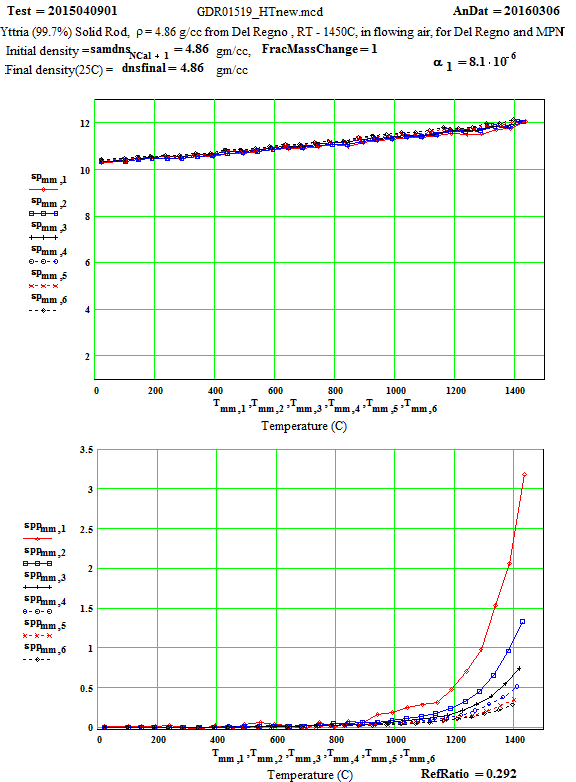
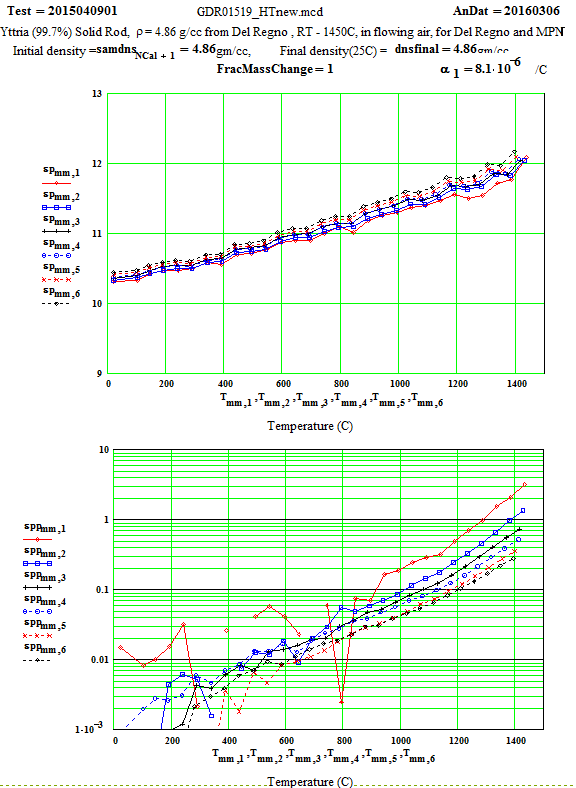
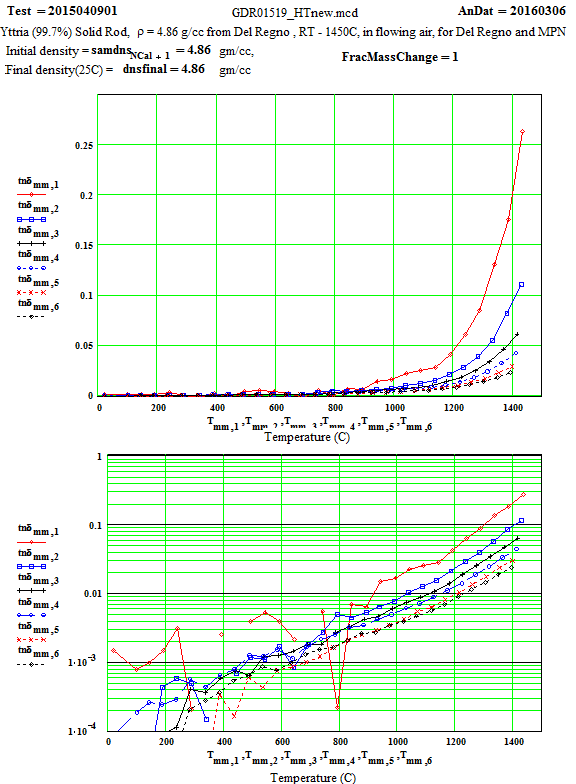
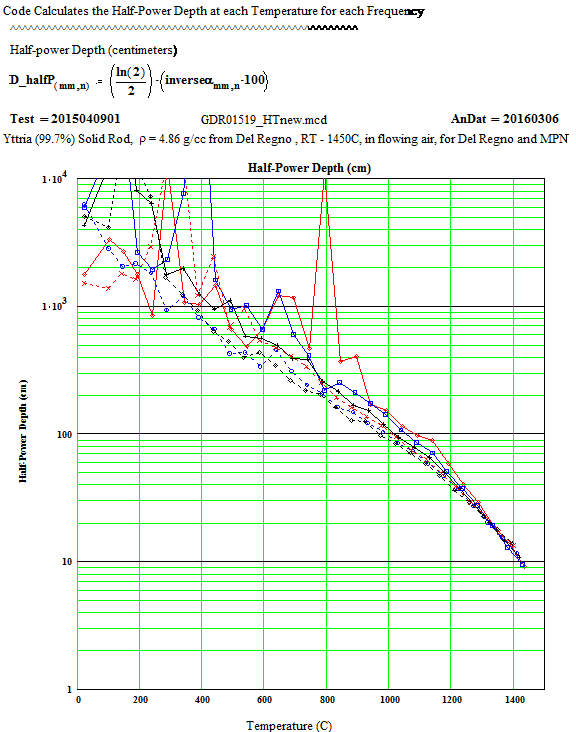
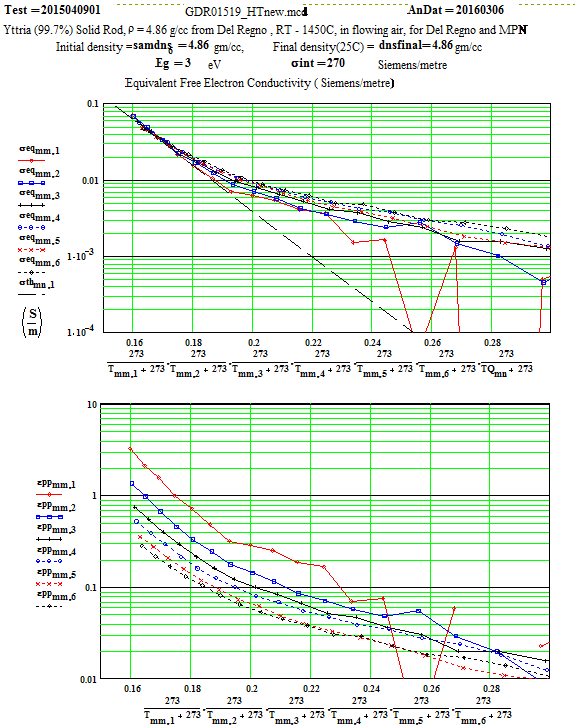
This plot includes the values measured while the temperature was decreasing from 1450C .